Question

Of the students in a certain homeroom, 9 are I the school play, 12 are in the orchestra, and 15 arc in the choral group. If 5 students participate in exactly 2 of 3 activities and all other students participate in only 1 activity, how many students are in the homeroom?A. 31B.30C. 26D.25

Answer 1

Let's use the variable S to represent the students that are in the school play, O for orchestra and C for the choral group.

If 5 students participate in exactly 2 of 3 activities, we have:

`\begin{gathered} N(S\cap O)\cup N(O\cap C)\cup N(C\cap S)=5 \\ N(S\cap O)+N(O\cap C)+N(C\cap S)-2\cdot N(S\cap O\cap C)=5 \end{gathered}`

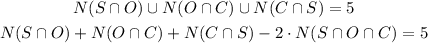
Since there are no students that participate in all three activities, we have:

`N(S\cap O\cap C)=0`

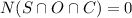
Then, to find the number of students in the homeroom, let's use the formula:

`\begin{gathered} N(S\cup O\cup C)=N(S)+N(O)+N(C)-N(S\cap O)-N(O\cap C)-N(C\cap S)+N(S\cap O\cap C) \\ N(S\cup O\cup C)=9+12+15-(N(S\cap O)+N(O\cap C)+N(C\cap S))+N(S\cap O\cap C) \\ N(S\cup O\cup C)=9+12+15-(5)+0 \\ N(S\cup O\cup C)=31 \end{gathered}`

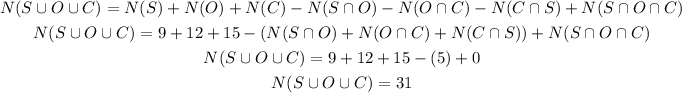
Therefore the correct option is A.