Since angle Cita lies on the 2nd quadrant, then
The value of tan Cita is negative
Let us use the identites
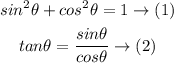
Since sin Cita = 4/5, then substitute it in (1)
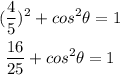
Subtract 16/25 from each side
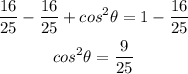
Take a square root for both sides
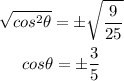
Since Cita lies in the 2nd quadrant, then its cosine is negative
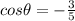
Now, use identity (2) to find tan Cita
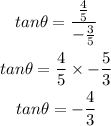
The answer is
tan Cita = -4/3