Question

Determine the angle of rotation of the conic section given by: 17x2 +32xy – 7y2 = 75 (round your answer to the nearest tenth of adegree).

Answer 1

To find the angle of rotation of a conic section, we have fisrs to see the following form of the equation:

`Ax^2+Bxy+Cy^2+Dx+Ey+F=0`

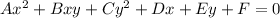
Given thah form, we can find the angle of rotation by the equation:

`\tan 2\theta=(B)/(A-C)`

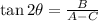
From first the given section:

`17x^2+32xy-7y^2=75`

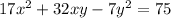
We get that A = 17, B = 32 and C = -7. So,

`\begin{gathered} \tan 2\theta=(32)/(17-(-7))=(32)/(24)=(4)/(3) \\ 2\theta=\arctan ((4)/(3))=53.1\degree \\ \theta=26.6\degree \end{gathered}`

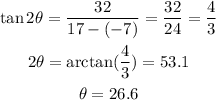
The angle of the first given section is 26.6°.

Now, for the second one:

`32x^2+50xy+7y^2=100`

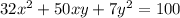
We have A = 32, B = 50 and C = 7, so:

`\begin{gathered} \tan 2\theta=(50)/(32-7)=(50)/(25)=2 \\ 2\theta=\arctan 2=63.4\degree \\ \theta=32.7\degree \end{gathered}`

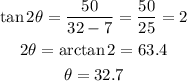
The angle of the second given section is 32.7°.