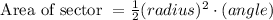1 Answer

Akbertram · Answer 1 · 2023-05-23T10:43:10+0000

For solving this problem we need to remember the generic formula. If we have a circle sector with angle x (in degrees),

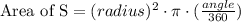
$\text{Area of S}=(radius)^2\cdot\pi\cdot((angle)/(360))$

The trick of this exercise is that our angle is expressed in degrees (°). Be careful!

Let's compute the solution:

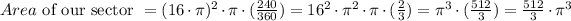
$Area\text{ of our sector }=(16\cdot\pi)^2\cdot\pi\cdot((240)/(360))=16^2\cdot\pi^2\cdot\pi\cdot((2)/(3))=\pi^3\cdot((512)/(3))=(512)/(3)\cdot\pi^3$

That's the final answer.

Comment: For every exercise of this kind you only need to apply the formula I provided you above. If the angle is in radians, the formula is

$\text{ Area of sector }=(1)/(2)(radius)^2\cdot(angle)$

Please log in or register to add a comment.