Question

The sum of three numbers is 17. Two times the smallest is 4 less than the largest, while the sum of the largestand smallest is 13. Use a linear system in three variables to find the three numbers.The three numbers are_____, ______and______.

Answer 1

`x=10,y=4,z=3`

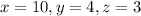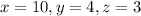
1) Let's carefully read the statements so that we write accurate equations.

"The sum of three numbers is 17"

x+y+z=17

"Two times the smallest is 4 less than the largest"

2z=x-4

" the sum of the largest and smallest is 13"

x+z=13

Note that we have stated the largest one to be "x" and the smallest one to be "z"

2) Setting this Linear system we have:

`\begin{gathered} \mleft\{\begin{matrix}x+y+z=17 \\ 2z=x-4 \\ x+z=13\end{matrix}\mright. \\ \end{gathered}`

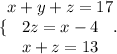
Now, let's solve it by performing some algebraic manipulations:

`\begin{gathered} \{\begin{matrix}x+y+z=17 \\ 2z-x-4 \\ x+z=13\end{matrix} \\ -x+2z=-4 \\ x+z=13 \\ -------- \\ 3z=9 \\ (3z)/(3)=(9)/(3) \\ z=3 \\ x+3=13 \\ x+3-3=13-3 \\ x=10 \\ x+y+z=17 \\ 10+y+3=17 \\ 13+y=17 \\ 13+y-13=17-13 \\ y=4 \end{gathered}`

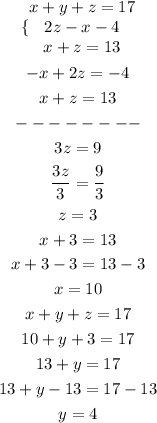
Note that we started solving two equations and then plugging the result into original equations, we ended up finding the variables.

Thus the answer is:

`x=10,y=4,z=3`