We have to estimate and then calculate the proportion, in percentage, of the flag is the union area.
We can estimate the area of the union as:
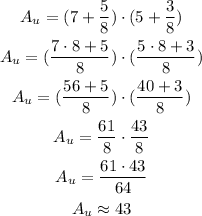
Then, we can now calculate the area of the flag as:
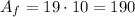
We can now estimate the percentage as:
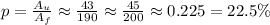
We can now calculate the values with a calculator as:
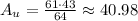
Then, the percentage is:
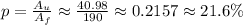
Answer:
The estimated percentage was 22.5%.
The actual percentage is 21.6%.