Question

The electrical power produced by a Winter vine as a function of the speed of the wind the function POV equals 1.1 670 cubed where the represents the speed of the wind in meters per second and POV represents the electrical power produced in kilowatts describes this relationship how strong is the wind is required to produce 400 kW of electricity.

Answer 1

7 m/s

Step-by-step explanation:

We know that the electrical power produced and the speed of the wind are related by:

`P(v)=1.167v^3`

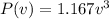
Then, if the electrical power produced is 400 kW, we can write the following equation:

`400=1.167v^3`

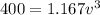
So, we need to solve the equation for v to know the speed of the wind.

`\begin{gathered} 1.167v^3=400 \\ (1.167v^3)/(1.167)=(400)/(1.167) \\ v^3=342.76 \\ v=\sqrt[3]{342.76}=6.99\approx7 \end{gathered}`

Therefore, the speed of the wind is approximately 7 m/s