We want to do the following operation:
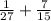
To add fractions, we need to put both denominators in the same value. We need to find the LCM between 27 and 15. Factorizing those numbers in prime numbers, we have:
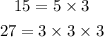
The LCM is the result of multiplying all those prime factors the most times they occur. Since 3 appears on both factorizations, we'll use only the most occuring 3(in this case, 3 times).
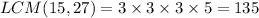
Now, we need to rewrite those fractions with the new denominator. To do that we just need to multiply both the numerator and the denominator by the same factor. To find those factors we just need to find the ratio between the denominator and 135.
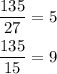
Now, converting those fractions to this denominator:
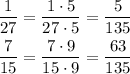
Now, to finally do the addition, we just add the numerators.
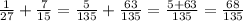
Since 68 and 135 don't share any divisors, this is the simplest form of this fraction. The result is 68/135.