Given
Confidence level = 90% = 0.90
green peas = 414
yellow peas = 155
Find
Estimate of the percentage of yellow peas.
Step-by-step explanation
Confidence level = 90% = 0.90
number of successes = 155
sample size = 414 + 155 = 569
so ,
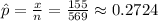
for confidence level ,
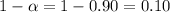
so ,
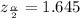
margin of error =
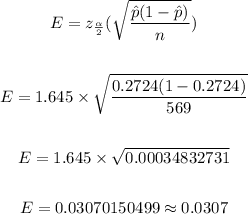
boundaries of the confidence level are

Final Answer
Hence , the estimate of the percentage of yellow peas is between 0.242 and 0.303