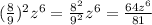Question

I need to know what this question means and how do i get the answer

Answer 1

In this problem, we need to create an expression that after applying one of the properties of exponents to simplify it, we obtain the given answer.

The first answer we have is:

`8^(2/9)`

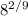
The second one is:

`(x^4)/(y^2)`

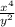
The third one is:

`(64z^6)/(81)`

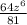
a. The first property is the product of powers:

`a^m\cdot a^n=a^(m\cdot n)`

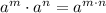
In the first answer, we have the exponent 2/9, and we can express it as:

`(2)/(9)=(1)/(9)+(1)/(9)`

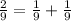
Then, the expression can be:

`8^(1/9)\cdot8^(1/9)\text{ which is equal to }8^(2/9)`

For the second answer we can rewrite the expression as:

`(x^2\cdot x^2)/(y\cdot y)\text{ and when we apply the product property we obtain}(x^4)/(y^2)`

For the third answer, we have:

`(64z^2\cdot z^4)/(81)\text{ which is equal to}(64z^(2+4))/(81)=(64z^6)/(81)`

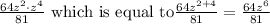
b. Power of a power property:

`(a^m)^n=a^(m* n)`

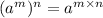
First answer:

`(8^2)^(1/9)=8^(2*1/9)=8^(2/9)`

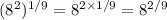
Second answer:

`((x^2)^2)/(y^2)=(x^(2*2))/(y^2)=(x^4)/(y^2)^{}`

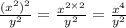
Third answer:

`(64(z^3)^2)/(81)=(64z^(3*2))/(81)=(64z^6)/(81)`

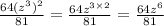
c. Power of a product:

`a^mb^m=\mleft(ab\mright)^m`

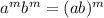
First answer:

`4^(2/9)\cdot2^(2/9)=(4\cdot2)^(2/9)=8^(2/9)`

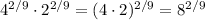
Second answer:

`(\frac{x^{}}{y})^2\cdot(x)^2=((x)/(y)\cdot x)^2=((x\cdot x)/(y))^2=(\frac{x^2^{}}{y})^2=(x^4)/(y^2)^{}`

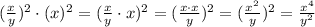
Third answer:

`((8)/(9))^2\cdot(z^3)^2=((8)/(9)\cdot z^3)^2=(64z^6)/(81)`

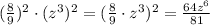
d. Negative exponent:

`a^(-m)=(1)/(a^m)`

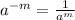
First answer:

We can express the exponent as:

`\begin{gathered} 2*9^(-1)=2*(1)/(9)=(2)/(9) \\ \text{Then:} \\ \text{ 8\textasciicircum(2}\cdot9^(-1))=8^(2/9) \end{gathered}`

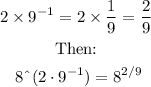
Second answer:

`x^4* y^(-2)=x^4*(1)/(y^2)=(x^4)/(y^2)`

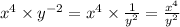
Third answer:

`64z^6*9^(-2)=64z^6*(1)/(9^2)=64z^6*(1)/(81)=(64z^6)/(81)`

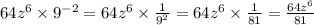
e. Zero exponent:

`a^0=1,a\\e0`

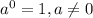
First answer:

`x^08^(2/9)=1*8^(2/9)=8^(2/9)`

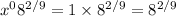
Second answer:

`(2^0x^4)/(y^2)=(1* x^4)/(y^2)=(x^4)/(y^2)`

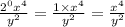
Third answer:

`\frac{64z^6x^0^{}}{81}=(64z^6*1)/(81)=(64z^6)/(81)`

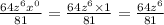
f. Quotient of powers:

`(a^m)/(a^n)=a^(m-n)`

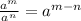
First answer:

`(8^(3/9))/(8^(1/9))=8^(3/9-1/9)=8^(2/9)`

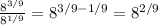
Second answer:

`(x^6)/(x^2y^2)=(x^(6-2))/(y^2)=(x^4)/(y^2)`

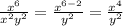
Third answer:

`(64z^8)/(81z^2)=(64z^(8-2))/(81)=(64z^6)/(81)`

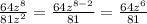
g. Power of a quotient:

`((a)/(b))^m=(a^m)/(b^m)`

First answer:

`\frac{16^(2/9)^{}}{2^(2/9)}=((16)/(2))^(2/9)=8^(2/9)`

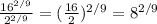
Second answer:

`((x)/(y))^2x^2=(x^2)/(y^2)\cdot x^2=(x^2\cdot x^2)/(y^2)=(x^4)/(y^2)`

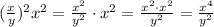
Third answer:

`((8)/(9))^2z^6=(8^2)/(9^2)z^6=(64z^6)/(81)`