Question

Use the graph to find the domain of F, the range of F, The X intercepts, the Y intercept, the intervals on which F is increasing and decreasing, The intervals on which F is constant and The number at which F has a relative minimum. What are the zeros of the function. What is the value of f(-1).x-values where f(x) = 3. Is F odd, even or neither.

Answer 1

The domain of a function is all values of x the function can assume.

Looking at the graph, we can see that the function can assume any real value for x, so the domain in interval notation is:

`(-\infty,\infty)`

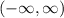
The range of a function is all values of y the function can assume.

Looking at the graph, the minimum value of y the function can assume is -1, and there is no maximum value (it goes towards positive infinity), therefore the range is:

`\lbrack-1,\infty)`

The x-intercepts are the points where the graph intersects the x-axis (where y = 0).

Looking at the graph, the x-intercepts are (2, 0) and (4, 0).

The y-intercepts are the points where the graph intersects the y-axis (where x = 0).

Looking at the graph, the y-intercept is (0, 8).

The interval where F is increasing is:

`(3,\infty)`

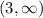
The interval where F is constant is:

`(-\infty,0)`

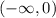
The interval where F is decreasing is:

`(0,3)`

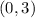
The minimum point of the function is (3, -1), so the number at which F has a relative minimum is x = 3 and the relative minimum is y = -1.

The zeros of a function are the values of x where y = 0 (the zeros are the x-coordinates of the x-intercepts).

So the zeros are 2 and 4.

f(-1) is the value of the function for x = -1.

Looking at the graph, for x = -1 the function value is 8, so f(-1) = 8.

In order to find the x-values for f(x) = 3, we need to find the values of x for y = 3.

Looking at the graph, the value y = 3 can be found when x = 1 and x = 5.

Therefore the leftmost x-value is x = 1 and the rightmost x-value is x = 5.

Odd functions have the property:

f(x) = -f(-x).

These functions are symmetric about the origin.

Even functions have the property:

f(x) = f(-x).

These functions are symmetric about the y-axis.

Looking at the graph, function F is neither odd nor even.