Question

As a train accelerates away from a station, it reaches a speed of 4.7m/s in 5.0s. if the train acceleration remains constant, what is its speed after an additional 6.0s had elapsed?

Answer 1

Given:

Speed, v = 4.7 m/s

Time, t = 5.0 s

Let's find the speed of the train after an additional 6.0 seconds had elapsed.

Apply the motion equation:

`v=u+at`

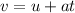
Where:

v is the final speed of the train

u is the initial velocity = 0 m/s

t is the total time = 5.0s + 6.0s = 11.0s

a is the acceleration.

To find the accelaration for the first 5 seconds, we have:

`\begin{gathered} a=(v)/(t) \\ \\ a=(4.7)/(5)=0.94m/s^2 \end{gathered}`

Here, we are told the acceleration(a) remains constant.

Hence, to find the speed after an additional 6.0s had elapsed, we have:

`v^(\prime)=u+at^(\prime)`

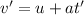
Where:

u = 0 m/s

a = 0.94 m/s²

t' = 11.0s

Thus, we have:

`\begin{gathered} v^(\prime)=0+0.94\ast11 \\ \\ v^(\prime)=10.34\text{ m/s} \end{gathered}`

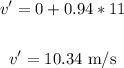
Therefore, the speed after an additional 6.0s had elapsed is 10.34 m/s.

ANSWER:

10.34 m/s