Question

I need help with this question please and thank you

Answer 1

First, let's simplify the left part of the equation using the following properties:

`\begin{gathered} (a^b)/(a^c)=a^(b-c) \\ (a^b)^c=a^(b\cdot c) \end{gathered}`

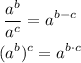
So we have:

`(\frac{13^0^{}}{13^3})^{(1)/(3)}=(13^(0-3))^{(1)/(3)}=(13^(-3))^{(1)/(3)}=13^{-3\cdot(1)/(3)}=13^(-1)`

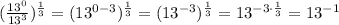
The statement is wrong because the exponent of the numerator is 0 and not 1, like the exponent on the second given equation (which is correct), so the result is different.