ANSWER
A) one-third
B) two-thirds
Step-by-step explanation
FIRST QUESTION
The volume of a cone is given as:

and the volume of a cylinder is given as:
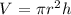
where r = radius
h = height
If a cone has the same radius and height as a cylinder, it means that r = r and h = h.
Therefore, comparing the volumes, we have that the volume of the cone will be 1/3 of the volume of the cylinder.
The correct option is one-third.
SECOND QUESTION
The volume of a sphere is given as:

We have already stated the volume of a cylinder above.
If the height of a cylinder is twice its radius, it means:
h = 2r
Therefore:
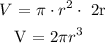
If the radius of a cylinder and sphere are the same, it means r = r.
Therefore, comparing the volumes, we see that the volume of the sphere is 2/3 times that of a cylinder.
The correct option is two-thirds.