Question

Write an equation for a parabola with a vertex of (-2,1) and a focus of (-2,4)

Answer 1

`y=(1)/(12)(x+2)^(2)+1`

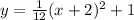
Explanation:

Given a parabola with the following properties:

• Vertex: (-2, 1)

,

• Focus: (-2, 4)

We want to write an equation for the parabola.

The standard equation of an up-facing parabola with a vertex at (h,k) and a focal length |p| is given as:

`\begin{equation}(x-h)^(2)=4 p(y-k)\end{equation}`
`\begin{gathered} Vertex,(h,k)=(-2,1)\implies h=-2,k=1 \\ Focus,(h,k+p)=(-2,4)\implies h=-2,k+p=4 \end{gathered}`

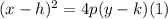
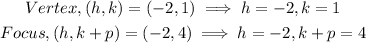
We solve for p:

`\begin{gathered} k+p=4 \\ 1+p=4 \\ p=4-1 \\ p=3 \end{gathered}`

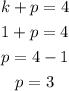
Substitute the values h=-2, k=1, and p=3 into the standard form given earlier:

`\begin{gathered} (x-(-2))^2=4(3)(y-1) \\ (x+2)^2=12(y-1) \\ \text{ Divide both sides by 12} \\ (1)/(12)(x+2)^2=y-1 \\ \text{ Add 1 to both sides of the equation} \\ y=(1)/(12)(x+2)^2+1 \end{gathered}`

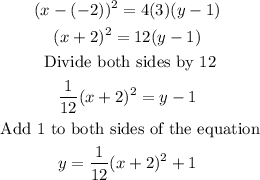
The equation for the parabola is:

`y=(1)/(12)(x+2)^(2)+1`

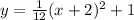
The last option is correct.