Explanation
We are given the following information:
• A local magazine charges $5 per copy and sells approximately 1000 copies.
,
• The magazine expects to sell 100 copies more for every $0.25 reduction in price.
We are required to determine:
• The maximum revenue that the magazine can expect for each issue.
,
• The price per copy that will maximize revenue.
First, we need to determine the number of copies and the price per copy as follows:
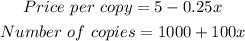
Next, we determine the revenue as:
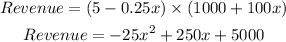
Showing this function in a graph, we have:
The maximum revenue that the magazine can expect for each issue is represented in the graph as:
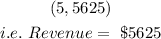
The price per copy that will maximize revenue is:
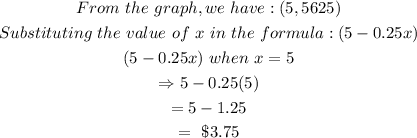
Hence, the answers are:
The maximum revenue that the magazine can expect for each issue is: $5,625
The price per copy that will maximize revenue is: $3.75