Question

The figure below shows a right circular cylindrical tube made out of paper. The circumference of each circular base is 10 centimeters, the length of AB is 12 centimeters, and BC is a diameter of a base. If the tube is cut along AB, opened, and flattened, what is the length of AC, in centimeters?

Answer 1

The distance between A and C in cm is

`AC=13`

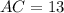
To solve this, we know that the tube is flattened to form a rectangle.

2 sides of the rectagle will have a lenght of 10cm, that correspont to the perimeter of the circumference. The other 2 sides will have a lenght of 12cm, corresponding to the lenght of AB, which is where we are making the cut.

Then we'll have something like this:

The point C divides the top side in two equal segments. This is because B and C are opposite points when the cillindrical tube is formed.

Now to find the lenght of C, we can use the Pythagorean Theorem. We can trace a line (the red one in the drawing) and now one leg of the right triangle will be 12cm and the other is half of 10cm = 5cm

Then:

`AC=\sqrt[]{12^2+5^2}=\sqrt[]{144+25}=\sqrt[]{169}=13`

Then the length of AC is 13