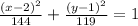Question

Determine the standard equation of the ellipse. Foci at (-3,1) and (7,1); vertex at ( - 10,1)

Answer 1

The equation of an ellipse has the following structure:

`((x-h)^2)/(a^2)+((y-k)^2)/(b^2)=1`

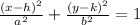
Where a is the major radius, b is the minor radius (when the ellipse is horizontal), and the center of the ellipse is located at the point (h,k).

We can say this ellipse is horizontal because the foci are located at the same height (1). Joining both of them will form a horizontal line coincident with the longest axis of the ellipse.

Both foci are equally distanced from the center, then we can estimate the coordinates of the center of the ellipse. We just need to find the midpoint between (-3,1) and (7.1). We already know that the y coordinate of the center is 1 because both foci and the center are located at the same horizontal line. For the x coordinate we just need to average the x coordinates of both foci:

`(-3+7)/(2)=(4)/(2)=2`

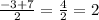
With this, we can say that the center of the ellipse is located at point 2,1. Then, h=2 and k=1.

We can calculate the major radius since we already know the center and one vertex. The major radius is the distance between those points. Since they are located at the same horizontal line (y=1), the distance between them is simply the difference in x coordinate. If one vertex is at (-10,1) and the center is at (2,1), the distance between them is (2-(-10)) = 12. Then, the major radius of the ellipse is a = 12. We just need to calculate the minor radius of the ellipse to be able to buld the equation.

There is certain relationship between major radius (a) minor radius (b) and the focal distance (c). The focal distance of the ellipse is measured from the senter to each focus. For this ellipse, its value will be 7-2=5.

The minor radius and focal distance form a right angle, and the distance from the foci to the upper part of the ellipse is equal to the major radius. Then, applying Pythagoras theorem to the triangle that is formed we can say:

`a^2=b^2+c^2`

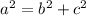
We can calculate b now, recalling that a=12 and c=5:

`\begin{gathered} b=\sqrt[]{12^2-5^5} \\ b=\sqrt[]{144-25} \\ b=\sqrt[]{119} \end{gathered}`

Then, the equation can be built with all the information now.

a = 12 -> a^2 = 144

b = √119 -> b^2 = 119

h = 2

k = 1

`((x-2)^2)/(144)+((y-1)^2)/(119)=1`