To be able to graph the function we have to find the vertex of the graph of the function and the axis of symmetry, we know that the domain are all real numbers and the range are all positive numbers including zero.
We start by finding the vertex:
we know that the absolute value function of any number is equal or greater than zero for all real numbers this implies that the graph has a vertex for:
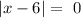
Solving for x we get:
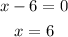
We conclude that the graph of the function has a vertex for x=6. On the other hand, notice that for x<6
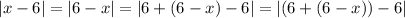
Then we can conclude that the graph of the function has a symmetry axis for x=6.
Finally we graph the function: