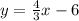Question

POSFind the equation of the line that is the perpendicular bisector of the segment with endpoints (2,5) and (10, -1).y =___x+___

Answer 1

To answer this question, we need to remember that a perpendicular bisector of a line segment passes through the midpoint of that segment, and it is perpendicular to it (they form 90° between them).

Then, we have:

1. The endpoints of the segment are:

(2, 5) and (10, -1)

2. We need to find the midpoint of this segment. For this, we have to apply the next formula:

`x_m=(x_1+x_2)/(2),y_m=(y_1+y_2)/(2)`

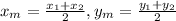
Then, we have that:

• (2, 5) ---> x1 = 2, y1 = 5

,

• (10, -1) ---> x2 = 10, y2 = -1

Therefore:

`x_m=(2+10)/(2)\Rightarrow x_m=(12)/(2)\Rightarrow x_m=6`

`y_m=(5+(-1))/(2)\Rightarrow y_m=(4)/(2)\Rightarrow y_m=2`

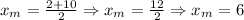
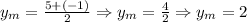
The midpoint of the segment is, therefore, (6, 2).

3. Now we need to find the slope of the given segment, so we can find later the slope of the perpendicular bisector. The slope of a line is given by:

`m=(y_2-y_1)/(x_2-x_1)`

And we already know that:

• (2, 5) ---> x1 = 2, y1 = 5

,

• (10, -1) ---> x2 = 10, y2 = -1

Then, the slope of this segment of a line is:

`m=(-1-5)/(10-2)\Rightarrow m=(-6)/(8)\Rightarrow m=-(3)/(4)`

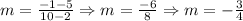
4. If two lines are perpendicular, then the product of their slopes is equal to -1:

`m_1\cdot m_2=-1\Rightarrow m_2=-(1)/(m_1)`

Therefore, if we know that the perpendicular bisector is perpendicular to the given segment, then the slope of that perpendicular bisector is:

`m_p=-(1)/(-(3)/(4))\Rightarrow m_p=(4)/(3)`

We can check the result if we multiply both slopes as follows:

`m_1\cdot m_p=-1\Rightarrow-(3)/(4)\cdot(4)/(3)=-1\Rightarrow-1=-1`

5. Now, we have the midpoint the perpendicular bisector passes through and its slope. Then, we can apply the point-slope formula for the line as follows:

`y-y_1=m(x-x_1)`

We have that the midpoint is (6, 2), and the slope is m = 4/3. Then, we have:

1. (6, 2) ---> x1 = 6, y1 = 2.

`y-2=(4)/(3)(x-6)\Rightarrow y-2=(4)/(3)x+(4)/(3)(-6)`

`y-2=(4)/(3)x-8`

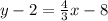
Adding 2 to both sides of the equation, we have:

`y-2+2=(4)/(3)x-8+2\Rightarrow y=(4)/(3)x-6`

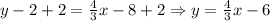
Therefore, the equation of the line that is the perpendicular bisector of the segment with endpoints (2, 5) and (10, -1) is:

y = (4/3)x - 6

Or

`y=(4)/(3)x-6`