The equation of the line is

Where m is the slope and b is the y-intercept
So, we must calculate the equation for this case
We have two points:
- (-2, 2)
- (0, -2)
The equation for the slope is
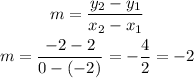
Then, we must calculate b using the value of the slope and one of the two points
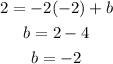
Therefore equation of the line will be,
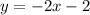
Now, we can see that the shaded region is the left part of the line
So the equation of the inequality will be
y <= -2x - 2