Find the measure of angles G and the length of GH

Question

asked Nov 21, 2023 90.6k views

1 Answer

Akd · Answer 1 · 2023-11-26T21:55:09+0000

Since △GHI is a right triangle, then, from the Pythagorean Theorem, the lengths of its sides satisfy the following equation:

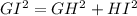
Where GI is the hypotenuse of the right triangle, and GH and HI are the legs of the right triangle.

Since GH is unknown, isolate it from the equation:

$GH=\sqrt[]{GI^2-HI^2}$

Substitute the values of GI and HI:

$\begin{gathered} GH=\sqrt[]{26^2-10^2} \\ =\sqrt[]{676-100} \\ =\sqrt[]{576} \\ =24 \end{gathered}$

Therefore, GH=24.

On the other hand, recall the definition of sine of an angle on a right triangle:

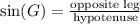
$\sin (G)=\frac{\text{opposite leg}}{\text{hypotenuse}}$

The leg opposite to G is HI, and the hypotenuse of the right triangle is GI. Then:

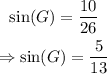
$\begin{gathered} \sin (G)=(10)/(26) \\ \Rightarrow\sin (G)=(5)/(13) \end{gathered}$

Take the inverse sine function from both sides:

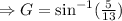
$\Rightarrow G=\sin ^(-1)((5)/(13))$

Use a calculator to find the inverse sine of 5/13:

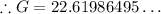
$\therefore G=22.61986495\ldots$

Therefore, the angle G is approximately 22.6°.