Question

35. The selling prices for homes in a certain community are approximately normally distributed with a mean of $321,000 and a standard deviation of $38,000. Estimate the percentage of homes in this community with selling prices (a) between $245,000 and $397,000. % (b) above $435,000. % (c) below $283,000. % (d) between $283,000 and $435,000. %

Answer 1

Given the selling prices for homes in a certain community are approximately normally distributed

Mean = μ = $321,000

Standard deviation = σ = $38,000

For the following cases, we will find the z-score as follows:

`z=(x-\mu)/(\sigma)`

And we will use the following chart:

Estimate the percentage of homes in this community with selling prices:

A) between $245,000 and $397,000

So, the z-score for the given prices will be:

`\begin{gathered} $245,000$\rightarrow z=(245000-321000)/(38000)=-2 \\ 397,000\rightarrow z=(397000-321000)/(38000)=2 \end{gathered}`

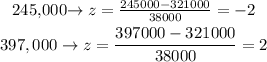
So, the percentage when -2 < z < 2 will be as shown from the chart = 95%

B) above $435,000

`435,000\rightarrow z=(435000-321000)/(38000)=3`

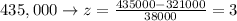
The area under the curve = 100%

So, the percentage when z > 3 will be = 0.5%

C) below $283,000

`283,000\rightarrow z=(283000-321000)/(38000)=-1`

so, the percentage when z < -1 will be = 50 - 34 = 16%

D) between $283,000 and $435,000

We will find the percentage in case if: -1 < z < 3

So, the percentage will be = 34 + 34 + 13.5 + 2 = 83.5%