Question

this question has multiple parts but im really lost so im just including everything, if possible help me find the part talking about linearization for tan, thank you!!

Answer 1

Given: A box with a square base and volume of 1200 cubic inches

To Determine: The dimension of the box

Solution

The box has a shape of a rectangular prism.

The volume of a box can calculated by the formula below

`\begin{gathered} Volume(box)=base-area* height \\ Area(square-base)=l^2 \\ Where:l=side-length \\ So, \\ Volume(box)=l^2h \end{gathered}`
`\begin{gathered} Volume(box)=1200in^3 \\ Therefore \\ l^2h=1200 \\ h=(1200)/(l^2) \end{gathered}`

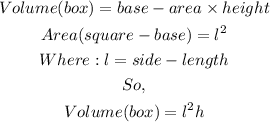
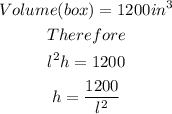
The area of the box is the addition of the area of the top and the bottom and the 4 sides

The top and the bottom are square in shape and the sides have the shape of a rectangle

Therefore, the area of the top and and bottom is

`\begin{gathered} Area(bottom)=l^2 \\ Area(top)=l^2 \\ Area-of-sides=4* h* l=4hl \end{gathered}`
`\begin{gathered} Area(top,and,bottom)=2* area(sides)===given \\ l^2+l^2=2*4hl \\ 2l^2=8hl \\ h=(2l^2)/(8l) \\ h=(l)/(4) \end{gathered}`

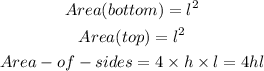
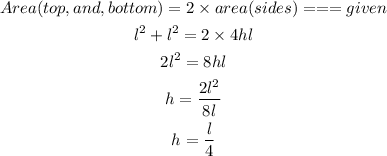
Since h is same, therefore

`\begin{gathered} (1200)/(l^2)=(l)/(4) \\ l^3=4800 \\ l=\sqrt[3]{4800} \\ l=16.87in \end{gathered}`
`\begin{gathered} h=(l)/(4) \\ h=(16.87)/(4) \\ h=4.22in \end{gathered}`

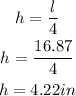
Hence, the dimension of the box are 16.87 inches by 16.87 inches by 4.22 inches