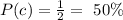Question

If you were flipping a fair coin, what is the probability of the following happening:a.Flipping it two times and getting 1 head and 1 tail (in any order)b.Flipping it three times and getting exactly 2 heads. c.Flipping it once and getting a tail if you’ve already flipped it five times and gotten 5 tails in a row

Answer 1

Explanation:

The probability is represented by the following equation:

`P=\frac{Number\text{ of favorable outcomes}}{Total\text{ number of possible outcomes}}`

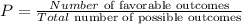
a) The probability of n tosses going 1 H and 1 Tail in 2 times is:

`\begin{gathered} P=(1)/(4)+(1)/(4)=(1)/(2) \\ P=\text{ 50\%} \end{gathered}`

b) for flipping it three times and getting exactly two heads:

Sample: {HHH, HTH, THH, TTH, HHT, HTT, THT, TTT} Therefore, the total number of possible outcomes is 8.

`\begin{gathered} P(B)=P(\text{ getting two heads\rparen+ P\lparen getting 3 heads\rparen} \\ P(B)=(3)/(8)+(1)/(8) \\ P(B)=(4)/(8)=(1)/(2)=\text{ 50\%} \end{gathered}`

c. For flipping it once and getting a tail if you've already flipped it five times and gotten 5 tails in a row.

The prior flipping does not affect the result of the new toss, they are not dependent events.

`P(c)=(1)/(2)=\text{ 50\%}`