Question

A right rectangular prism has a volume of 6x^2 - 3x^2 - 45x. What are the expressions for the length, width, and height? And what is the least possible integer value of x for the rectangular solid to exist? Explain.

Answer 1

Step 1. The expression that we have for the volume of the rectangular prism is:

`6x^3-3x^2-45x`

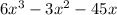
For part a, we need to find the expressions for the length, the width, and the height.

Step 2. The first step is to factorize the common factor which is 3x:

`6x^3-3x^2-45x=3x(2x^2-x-15)`

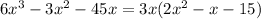
Step 3. The expression for the volume now is:

`(3x)(2x^2-x-15)`

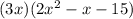
We can still factor the expression in the second parentheses so we will focus on that in this step.

• Factoring

`2x^2-x-15`

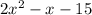
We will factor it to have the general form:

`(x-x_1)(x-x_2)`

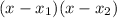
And to find x1 and x2, we use the quadratic formula:

`\begin{gathered} For\text{ an expression} \\ ax^2+bx+c \\ We\text{ use the quadratic formula:} \\ x_(1,2)=\frac{-b\pm\sqrt{b^(^2)-4ac}}{2a} \end{gathered}`

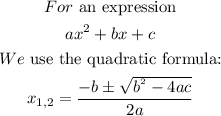
In this case:

`\begin{gathered} 2x^(2)-x-15 \\ \downarrow\downarrow \\ a=2 \\ b=-1 \\ c=-15 \end{gathered}`

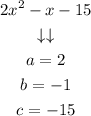
Substituting these values into the quadratic formula:

`\begin{gathered} x_(1,2)=(-(-1)\pm√((-1)^2-4(2)(-15)))/(2(2)) \\ Solving\text{ the operations:} \\ x_(1,2)=(1\pm√(1+120))/(4) \\ x_(1,2)=(1\pm√(121))/(4) \\ x_(1,2)=(1\pm11)/(4) \end{gathered}`

We find the two solutions using the + and the - sign:

`\begin{gathered} x_1=(1+11)/(4)=(12)/(4)=3 \\ x_2=(1-11)/(4)=-(10)/(4)=-2.5 \end{gathered}`

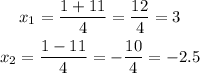
Then, the factored expression is:

`2x^2-x-15=(x-3)(x+2.5)`

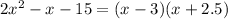
Step 4. Remember that the expression after we factored the common term was:

`(3x)(2x^(2)-x-15)`

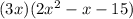
To this, we now substitute the factored form of the second expression:

`(3x)(x-3)(x+2.5)`

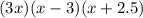
Step 5. Each pair of parentheses represents a dimension of the rectangular prism:

`\begin{gathered} length:\text{ 3x} \\ width:\text{ x}-3 \\ height:\text{ x+2.5} \end{gathered}`

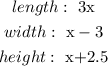
We have solved part a.

Step 6. In part b we need to find the least possible integer for the value of x.

This is simply that each expression for the length, width, and height that we found in step 5, must be greater than 0. That is because if one dimension is 0, there would be no volume.

`\begin{gathered} 3x>0 \\ x-3>0 \\ x+2.5>0 \end{gathered}`

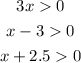
Solving each inequality:

`\begin{gathered} x>0/3\rightarrow x>0 \\ x>3 \\ x>-2.5 \end{gathered}`

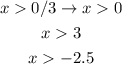
x has to be greater than 0, greater than -2.5 and greater than 3, therefore the least possible integer to that it meets all of the conditions is

x=4.

Answer:

Part a:

length: 3x

width: x-3

height: x+2.5

Part b:

x=4