Question

I open a valve in my rain barrel in my water garden. Every five minutes the volume of water in the barrel decreases by 10.5 gallons find and interpret the rate of change? and find the percentage change?

Answer 1

Let's suppose that the rain barrel starts with 100 gallons. Then, after 5 minutes, the barrel is left with 89.5 gallons. After 10 minutes, the barrel has 79 gallons. We can find the rate of change with this information:

`\begin{gathered} (x_1,y_1)=(5,89.5) \\ (x_2,y_2)=(10,79) \\ \Rightarrow m=(y_2-y_2)/(x_2-x_1)=(79-89.5)/(10-5)=(-10.5)/(5)=-2.1 \end{gathered}`

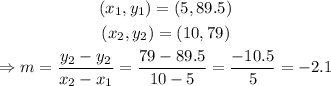
therefore, the rate of change is -2.1.

The percentage change from 100 to 89.5 is:

`\begin{gathered} \frac{\text{new value - old value}}{100} \\ \Rightarrow(89.5-100)/(100)=-0.105 \end{gathered}`

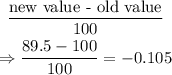
finally, we have that the percentage change is a decrease of 10.5%