Givens.
• Radius = 0.26 m.
,
• Frequency = 51 rev/min.
The period is the inverse of the frequency
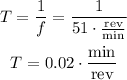
Then, we transform it into seconds.
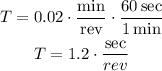
The period in seconds is 1.2.
Then, the tangential speed formula is
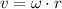
Where omega represents the angular speed, which in this case can be found using the frequency.
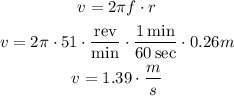
Therefore, the tangential speed is 1.39 meters per second.