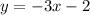Given:
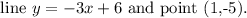
Aim:
We need to find the line which is parallel to y=-3x+6.
Step-by-step explanation:
We know that the slope of the parallel lines is equal.
The given line is of the form
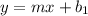
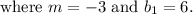
The slope of the required line is -3.
The slope-intercept form of the line equation for the required line is

substitute m=-3, x=1, and y=-5 in the equation to find the value of b.
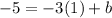
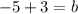
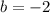
Substitute m=-3 and b= -2 in the slope intercept line equation.
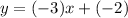
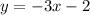
Final answer:
Teh slope-intercept equation is