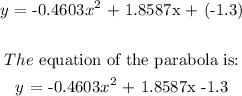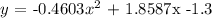
Step-by-step explanation:
When given a parabola and we want to get its equation, we will pick three points on the parabola. To make it easy, two of the points should be the x and y -intercept
Picking three points from the parabola:
x-intercept: (0.9, 0)
y-intercept: (0, -1.3)
3rd point: (1.4, 0.4)
Next we will insert the value above into the general formula for a parabola (quadratic function).
The formula is given as:
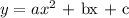

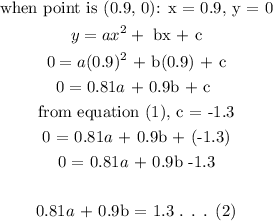
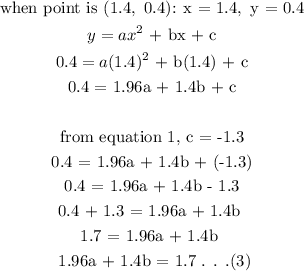
To get a and b, we will solve equation (2) and (3) simultaneously:
0.81a + 0.9b = 1.3 (2)
1.96a + 1.4b = 1.7 (3)
Using elimination method:
let's eliminate b. To do this we will multiply equation (2) by 1.4 and equation (3) by 0.9.
By so doing they will both have same coefficient in b and we will be able to do the eilmination
1.134a + 1.26b = 1.82 (2*)
1.764a + 1.26b = 1.53 (3*)
subtract equation (2*) from equation (3*):
1.764a - 1.134a + 126b - 126b = 1.53 - 1.82
0.63a = -0.29
divide both sides by 0.63:
a = -0.29/0.63
a = -0.4603
substitute for a in any of the equations:
using equation (2): 0.81a + 0.9b = 1.3

We will substitute the values of a, b, and c in the formula. The equation of the parabola will become: