Question

How many pounds of walnuts that cost $.80/# must be mixed with 8 pounds of cashews that cost $1.25/# to make a mixture of nuts that cost $1.00/#

Answer 1

Let 'w' be the pounds of walnuts and 'c' the pounds of cashews. Since we want to mix 8 pounds of cashews with some number of pounds of walnuts that cost $1, we have the expression:

`1(w+8)=w+8`

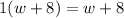
that represents the total mixture of nuts. We also know that each pound of walnut costs 0.8 and each pound of cashews cost 1.25, then:

`0.8w+1.25c`

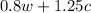
since c=8, we have the following:

`\begin{gathered} 0.8w+1.25\cdot8 \\ \Rightarrow0.8w+10 \end{gathered}`

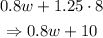
The total cost of the mix must be the sum of the total cost of the walnuts and the total cost of the cashews. Now we can use both equations to get w:

`\begin{gathered} w+8=0.8w+10 \\ \Rightarrow w-0.8w=10-8 \\ \Rightarrow0.2w=2 \\ \Rightarrow w=(2)/(0.2)=10 \\ w=10 \end{gathered}`

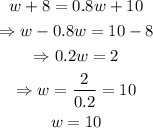
therefore, there must be 10 pounds of walnuts in the mixture