Question

After winning the free-throw competition Lebron decides to really rub it in by showing off some real skill. He grabs the ball, runs up the court, does a cart wheel then 3 bigps and jumps 11.2 m straight in the air, (all while doing a backflip and winking at the camera). His combined mass with the ball is 80.6 kg. What is Lebron's speed as beim dunks (basketball net is 3.0m off the ground)? (Assume no loss of energy)

Answer 1

Given data:

* The maximum height of Lebron is h_i = 11.2 m.

* The height of the basketball net is h_f = 3 m.

* The mass of Lebron with the ball is m = 80.6 kg.

Solution:

The initial velocity of Lebron at the maximum height is zero.

The change in the potential energy of Lebron is,

`dU=\text{mgh}_i-\text{mgh}_f`

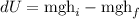
The change in the kinetic energy of the Lebron is,

`\begin{gathered} dK=(1)/(2)mv^2-(1)/(2)mu^2 \\ dK=(1)/(2)mv^2-0 \\ dK=(1)/(2)mv^2 \end{gathered}`

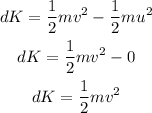
where v is the speed of Lebron as he slams dunk,

According to the law of conservation of energy,

`\begin{gathered} dU=dK \\ \text{mgh}_i-\text{mgh}_f=(1)/(2)mv^2 \\ gh_i-gh_f=(1)/(2)v^2 \\ g(h_i-h_f)=(1)/(2)v^2 \end{gathered}`

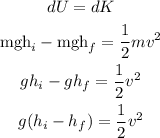
Substituting the known values,

`\begin{gathered} 9.8(11.2-3)=(1)/(2)v^2 \\ 9.8*8.2=(1)/(2)v^2 \\ v=\sqrt[]{2*9.8*8.2} \\ v=12.68\text{ m/s} \end{gathered}`

Thus, the velocity of Lebron in the given case is 12.68 meters per second.