Given:
No of people - 600
Rate:
Children - $ 1.25
Adults - $ 2.00
Total Admission - $ 1,021.50
Required:
No. of children and adults that day
Solution:
Let x - be the number of children
y - be the number of adults
We can write the expression for the total number of people in the pool as:
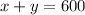
And the expression for the total admission is:
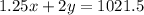
From the first equation we can write:
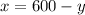
Now, we will substitute the expression for x into the second espression (for the total admission):
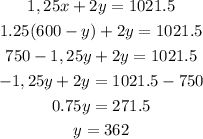
If y = 362, then x is:
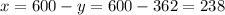
Answer:
There are 238 children and 362 adults in the pool that day.
To check:
Substiture the value of x and y into the second espression (for the total admission):
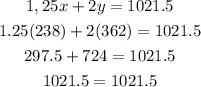
The computed value of x and y satisfies the second equation. Our answer is correct.