Question

A catering company is setting up for a wedding. They expect 150 people to attend. They can provide small tables that seat 6 people and large tables that seat 10 people.6b. Let x represent the number of small tables and y represent the numberof large tables. Write an equation to represent the relationship between xandy.*

Answer 1

From the statement, we know that:

• the catering company expect 150 people,

,

• they provide two kinds of tables,

,

• small tables seat 6 people,

,

• large tables seat 10 people.

We define the variables

• x = # of small tables,

,

• y = # of large tables.

From the info above, we see that:

• 6x is the number of people that x small tables can sit,

,

• 10y is the number of people that y large tables can sit.

The sum of 6x and 10y gives us the total number that we can sit and that number must be equal to 150:

`6x+10y=150.`

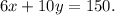
a) One possible combination is to choose:

• x = 10,

,

• y = 9.

We verify that the combination sum up 150 people

`6\cdot10+10\cdot9=60+90=150\text{ }✓`

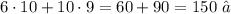
b) We previously have obtained the equation that represents the relation between x and y, that equation is:

`6x+10y=150.`

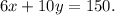
c) If we have the point (20, 5), we have:

• x = 20,

,

• y = 5.

We know that with 6 small tables and 10 larges tables we can sit:

`6x+10y\text{ people.}`

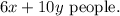
By replacing x = 20 and y = 5 we get:

`6\cdot20+10\cdot5=120+50=170.`

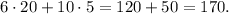
This result means that we can sit 170 people with (x, y) = (20, 5).

d) The equation that we wrote for this problem is:

`6x+10x=150.`

If we replace x = 20 and y = 5 we get:

`\begin{gathered} 6\cdot20+10\cdot5\questeq150, \\ 120+50\questeq150, \\ 170\\e150\text{ }✖ \end{gathered}`

We see that by replacing (x, y) = (20, 5) we obtain different numbers on both sides of the equation. So we conclude that the point (x, y) = (20, 5) is not a solution to the equation.

Answers

a) A possible combination is to have 10 small tables and 9 large tables.

b) The relation between x and y is given by the equation:

`6x+10y=150`

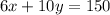
c) The point (x, y) = (20, 5) represents the situation where we can sit 170 people.

d) The point (x, y) = (20, 5) is not a solution to the equation.