Given:
There are given that the MN is the midsegment of the trapezoid ABCD.
Step-by-step explanation:
According to the question:
We need to find the value of segment AB:
So,
From the formula of a segment of midpoint:
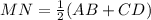
Then,
Put the value of the segment of MN and CD:
So,
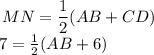
Then,
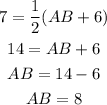
Final answer:
Hence, the correct option is A.