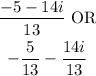SOLUTION:
Case: Complex number simplification
Given:
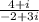
Required: To simplify the sum to a standard form for complex numbers
Method: Simplifaction by rationalization.
The rationalization process includes multiplying the top and bottom by the conjugate of the denominator i.e changing the separating operation to the opposite.
In this case the conjugate will be: (-2 - 3i)
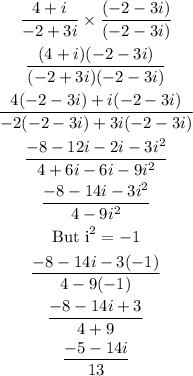
Final answer: