Question

Scientists have found a relationship between the temperature and the height above a distant planet's surface. T (h), given below, is the temperature inCelsius at a height of h kilometers above the planet's surface. The relationship is as follows.T(h) = 48.5 -2.5hComplete the following statements.

Answer 1

Given the equation:

`T\mleft(h\mright)=48.5-2.5h`

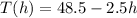
where: (h) is the height above the planet's surface in kilometers.

T(h) is the temperature in Celsius.

If we have calculated the function:

`h=T^(-1)(x)`

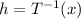
(a)

so, the output is the last function will be the height above the planet's surface.

So, the statements that best describe the last function is:

(b) the expression for the last function will be as follows:

`\begin{gathered} x=48.5-2.5h \\ 2.5h=48.5-x \\ h=(1)/(2.5)(48.5-x) \\ \\ h=19.4-0.4x \end{gathered}`

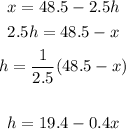
so, the answer for part (b) is:

`T^(-1)(x)=19.4-0.4x`

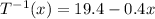
Part (c): we need to find:

`T^(-1)(33)=\text{?}`

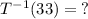
So, By substitution with x = 33 into the equation of part (a) as follows:

`\begin{gathered} T^(-1)(33)=19.4-0.4\cdot33 \\ \\ T^(-1)(33)=6.2 \end{gathered}`

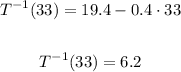
so, the answer of part (c) = 6.2