Answer:
Explanation:
Let us first convert the equation given into slope-intercept form for better understanding.
subtracting 4x from both sides gives
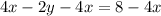
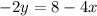
dividing both sides by -2 gives
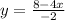
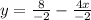
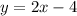
which is the equation in the slope-intercept form.
Now we are asked to find an equation that is parrallel to the above equation and passes through (-2, 1).
By parallel, we know that the new equation must have the same slope as the equation above (its slope must be 4).
Furthermore, we need to adjust the y-intercept such that the new equation passes through the point (-2,1).
Therefore, our equation will have the form
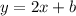
Now this equation passes through (-2, 1) meaning it should satisfy x = -2, y = 1.
Putting in x = -2 , y = 1 in the new equation gives
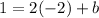
which simplifies to give
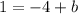
adding 4 to both sides gives
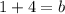
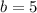
with the value of b in hand, we can now write our new equation
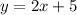
which is our answer!