Question

This is a Calculus 1 Problem. MUST SHOW ALL THE WORK AND JUSTIFICATION!!!Two friends, James and Jazmine meet at a pretzel stand in a large mall. Jazmine deciues she wants some new shoes, and leaves walking due East toward Foot Locker at 3 miles per hour. James wants to go to buy a new watch, but feels a rumble in his stomach. He decides to order a pretzel, and 3 minutes later leaves walking due North toward Dillard's at 3 miles per hour, happily munching on his pretzel. Assuming they are still walking, at what rate is the distance between them changing 12 minutes after?

Answer 1

4.2 mph

Explanation:

First, recall the formula below:

`Distance=Speed* Time`

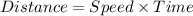
Let the number of hours for which they walked = t

Starting from the pretzel stand, Jazmine leaves walking due East toward Foot Locker at 3 mph.

`\text{ Distance covered by Jasmine after t hours}=3t\text{ miles}`

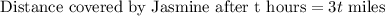
James 3 minutes later leaves walking due North toward Dillard's at 3 miles per hour.

`\text{ Distance covered by James after \lparen}t-0.05)\text{ hours}=3(t-0.05)\text{ miles}`

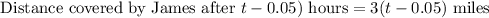
The diagram below illustrates the given information:

Using the Pythagorean theorem, we have that:

`x^2=(3t)^2+[3(t-0.05)]^2`

At t=12 minutes = 12/60 = 0.2 hours

`\begin{gathered} x^2=0.5625 \\ \implies x=√(0.5625)=0.75\text{ miles} \end{gathered}`

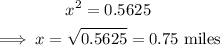
The distance, x between the two after 12 minutes is 0.75 miles.

Next, take the derivative of the equation:

`\begin{gathered} x^2=(3t)^2+[3(t-0.05)]^2 \\ Simplify \\ x^2=18t^2-0.9t+0.0225 \\ Take\;the\;derivative \\ 2x(dx)/(dt)=36t-0.9 \\ \implies(dx)/(dt)=(36t-0.9)/(2x) \end{gathered}`

At t=0.2 hours, x=0.75 miles

`(dx)/(dt)=(36(0.2)-0.9)/(2(0.75))=(6.3)/(1.5)=4.2\text{ miles per hour}`

The rate at which the distance between them is changing 12 minutes after is 4.2 miles per hour.