Question

Construct Arguments: Determine a valid conclusion from the given statement, if possible. Then state whether your conclusion was determined using the law of detachment or the Law of Syllogism. If no valid conclusion can be determined, select no valid conclusion. Justify your argument. If Terryl completes a course with a grade of C, then he will not receive credit. If Terryl does not receive credit, he will have to take the course again.

Answer 1

Law of Detachment

For the law of detachment to apply, you must have two statements. The first statement must be a conditional statement and the other, a non-conditional but supporting statement. The non-conditional statement must match the hypothesis of the first statement, which is conditional on arriving at a logical conclusion.

The law of detachment gives that:

`\begin{gathered} if\text{ p, then q} \\ \text{then} \\ q\text{ is the conclusion} \end{gathered}`

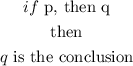
Law of Syllogism

In the rule of syllogism, there are three parts involved. Each of these parts is called a conditional argument. The hypothesis is the conditional statement that follows after the word if. The inference follows after the word then.

To represent each phrase of the conditional statement, a letter is used. The pattern looks like this:

`\begin{gathered} \text{Statement 1}\Rightarrow\text{ If p, then q} \\ \text{Statement 2}\Rightarrow\text{ If q, then r} \\ Conclusion\Rightarrow\text{ If p, then r} \end{gathered}`

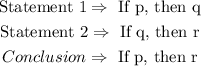
SOLUTION

Let's label the statements as follows:

`\begin{gathered} p=\text{ Terryl completes the course with a grade of C } \\ q=\text{ He will not receive credit} \\ r=\text{ He will have to take the course again} \end{gathered}`

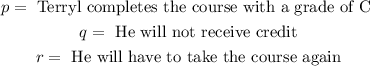
Therefore, the statements are:

`\begin{gathered} \text{if p, then q} \\ \text{if q, then r} \end{gathered}`

Hence, the conclusion is given using the Law of Syllogism:

`if\text{ p, then r}`

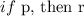
The conclusion is "If Terryl completes a course with a grade of C, then he will have to take the course again."