Question

What value of X and Y makes CDE. = HFG

Answer 1

Congruent triangles have the same measure of their angles, this implies that

`\angle E=\angle G`

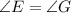
and they have exactly the same sides, this implies that

`DE=FG`

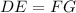
Since interior angles add up to 180 degrees, from triangle CDE, we get

`32+112+\angle E=180`

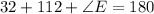
which gives

`\begin{gathered} 144+\angle E=180 \\ \angle E=180-144 \\ \angle E=36 \end{gathered}`

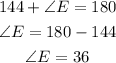
since angle G is equal to 4y+8, from our first relationship, we have

`36=4y+8`

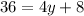
then, by moving 8 to the left hand side, we have

`\begin{gathered} 36-8=4y \\ 28=4y \end{gathered}`

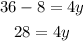
then y is given by

`\begin{gathered} y=(28)/(4) \\ y=7 \end{gathered}`

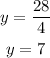
Now, by using our second relationship and the fact that DE=3x+2 and FG= 41, we have

`3x+2=41`

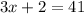
By moving 2 to the right hand side, wehave

`\begin{gathered} 3x=41-2 \\ 3x=39 \end{gathered}`

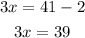
so, x is given by

`\begin{gathered} x=(39)/(3) \\ x=13 \end{gathered}`

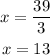
Therefore, the answers are x=13 and y=7