A right triangle needs to obey the Pythagora's theorem, that states:
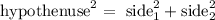
The square of the hypothenuse is equal to the sum of the squares of the sides. The hypothenuse is the largest side of the right triangle, so we can check if this is true for each case.
a) hypothenuse = 2.5, side1 = 2 and side2=1.5

This is a right triangle.
b) hypothenuse = 40, side1 = 32 and side2 = 24.
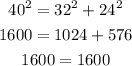
This is a right triangle.
c) hypothenuse = 15, side1 = 14 and side2 = 7.
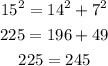
The equation is invalid and this is not a right triangle.
d) hypothenuse = 15, side1 = 9 and side2 = 12.
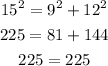
This is a right triangle.
The correct answer is "C".