we are given the following functions:
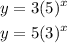
The graph of these equations is the following:
we are asked the following questions:
The y-intercept of both functions is the same. This is false since the y-intercept (the point where the graph touches the y-axis) for one of the functions is 3 and the other is 5.
The y-intercept of graph B is greater than the y-intercept of graph A. Since the y-intercept for graph A is 3 and the y-intercept for graph B is 5, this means that this statement is true.
Both graphs rise at the same rate. The rate of growth of an equation of the form:
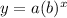
The rate of growth is the value of "b". The rate of growth for graph A is 5 and the rate of growth for graph B is 3, therefore, they are not the same.
Graph B rises faster than graph A. Since the rate of growth for graph A is 5 and the rate of growth for graph B is 3, this statement is false.
Graph A rises faster than graph B. This statement is true for the reason given above.
The y-intercept of graph A is greater than the y-intercept of graph B. This statement is false since the second statement is true.