Question

D) find the dimensions of the fence that given the maximum enclosed area

Answer 1

We have a fence as described in the picture.

The enclosed area is equal to x*y, while the fence perimeter is 2x+y.

As we know that the fence is 500 ft long, we can write:

`2x+y=500`

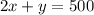
We have to maximize the area, subject to the constraint of the fence length of 500 ft.

We can use the constraint to replace y in the area equation:

`\begin{gathered} 2x+y=500 \\ y=500-2x \end{gathered}`
`xy=x(500-2x)=500x-2x^2`

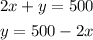
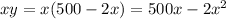
Then, we have this objective function we need to maximize:

`A(x)=500x-2x^2`

To maximize it we can derive A relative to x and equal it to 0 in order to find the value of x that maximizes A:

`\begin{gathered} (dA)/(dx)=0 \\ 500(1)-2(2x)=0 \\ 500-4x=0 \\ 500=4x \\ x=(500)/(4) \\ x=125 \end{gathered}`

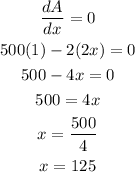
The value of y can be calculated as:

`\begin{gathered} y=500-2x \\ y=500-2(125) \\ y=500-250 \\ y=250 \end{gathered}`

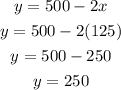
Answer:

b) The objective function is the enclosed area, and the constraint is the fence length F = 500 ft.

c) I choose to write the equation in terms of x and the objective function is 500x - 2x².

d) x = 125

y = 250