Question

Find the inverse of the function. Is the inverse a function?y=5x^2-3

Answer 1

C.

`y=\pm\sqrt[]{(x+3)/(5)}`

No, it is not a function

Explanation:

Given the below equation;

`y=5x^2-3`

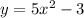
We'll follow the below steps to find its inverse;

Step 1: Switch the positions of x and y;

`x=5y^2-3`

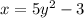
Step 2: Solve for y by first adding 3 to both sides of the equation;

`\begin{gathered} x+3=5y^2-3+3 \\ x+3=5y^2 \end{gathered}`

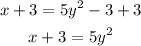
Step 3: Divide both sides by 5;

`\begin{gathered} (x+3)/(5)=(5y^2)/(5) \\ (x+3)/(5)=y^2 \end{gathered}`

Step 4: Take the square root of both sides;

`y=\pm\sqrt[]{(x+3)/(5)}`

The above is the inverse of the given function.

Note that in a function, each input is associated with exactly one output. Looking at the inverse of the function, we can see that some x values will yield two values of y, a negative and a positive value, therefore we can say that it is not a function since an input can produce more than one output value.

So the inverse of the function is not a function.