Given data:
1/50 or 0.02 of the policyholders - $20,000 claim
1/250 or 0.004 of the policyholders - $30,000 claim
1/500 or 0.002 of the policy holders - $60,000 claim
Find: expected value per policy sold
Solution:
The formula for expected value is:
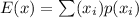
where E(x) = the expected value
xi = the value that x takes
p(xi) = the probability for that x value to occur.
Given the data that we have above, let's plug in those to the formula for expected value.
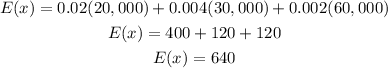
The expected value per policy is $640.