Question

The following table shows retail sales in drug stores in billions of dollars in the U.S. for years since 1995.YearRetail Sales085.8513108.4266141.7819169.25612202.29715222.266Let F(t) be the retails sales in billions of dollars in t years since 1995. A linear model for the data is F(t)=9.44t+84.182 .36912158090100110120130140150160170180190200210220Use the above scatter plot to decide whether the linear model fits the data well.The function is not a good model for the dataThe function is a good model for the data.Estimate the retails sales in the U. S. in 2012. billions of dollars. Round to the nearest whole number.Use the model to predict the year that corresponds to retails sales of $250 billion.

Answer 1

INFORMATION:

We have the following table that shows retail sales in drug stores in billions of dollars in the U.S. for years since 1995

We also have a linear model for the data

`F(t)=9.44t+84.182`

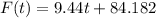
With the following scatter plot

And, we must solve the three questions.

STEP BY STEP EXPLANATION:

1.

To determine if the linear model fits the data well, we need to analyze the given scatter plot.

We can see that the blue points are very closed to the linear function, that means the function is a good model for the data.

2.

To estimate the retails sales in 2012, we must calculate which year is 2012 after 1995 and then replace it in the function.

So, we must subtract 1995 from 2012

`2012-1995=17`

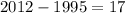
Now, replacing t = 17 in the function

`F(9)=9.44(17)+84.182=245`

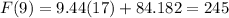
Then, in 2012 the retails sales were 245 billion of dollars

3.

To predict the year that corresponds to retail sales of 250 billion, we must equal the function to 250, and then solve it for t.

`\begin{gathered} 250=9.44t+84.182 \\ \text{ Solving for t,} \\ 250-84.182=9.44t \\ 165.818=9.44t \\ t=(165.818)/(9.44) \\ t=17.5655 \end{gathered}`

Finally, to find the year we must add 17 to 1995 which is the first year

`1995+17=2012`

Then, the year that corresponds to retail sales of 250 billion is 2012

ANSWER:

1. the function is a good model for the data.

2. 245

3. 2012