Question

Find the equation of a parabola with axis x= 1 and which also passes through the points (2, 1) and (3. -8)

Answer 1

y = -3x² + 6x + 1

Step-by-step explanation

The equation of a parabola in standard form is,

`y=ax^2+bx+c`

Where the x-coordinate of the vertex and, therefore, the axis of symmetry is,

`x=(-b)/(2a)`

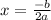
We know that this parabola has the axis of symmetry x = 1 and we also know what points it passes through, so we know that when x = 2, y = 1, and when x = 3, y = -8. With this information we have a system of 3 equations with 3 variables: a, b, and c:

• With the equation for vertex we have,

`1=(-b)/(2a)\Rightarrow b=-2a`

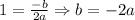
• With the point (2, 1) we have the equation,

`1=a\cdot2^2+b\cdot2+c\Rightarrow1=4a+2b+c`

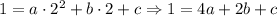
• And with the point (3, -8) we have the equation,

`-8=a\cdot3^2+b\cdot3+c\Rightarrow-8=9a+3b+c`

So, we have the system,

`\begin{cases}(1)\text{ }{b=-2a} \\ (2)\text{ }{1=4a+2b+c} \\ (3)\text{ }{-8=9a+3b+c}\end{cases}`

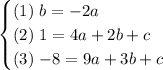
We can subtract the 2nd equation from the 3rd,

`\begin{gathered} 1-(-8)=(4a-9a)+(2b-3b)+(c-c) \\ \\ 9=-5a-b \end{gathered}`

Replace b with the first equation,

`\begin{gathered} 9=-5a-(-2a) \\ 9=-5a+2a \\ 9=-3a \end{gathered}`

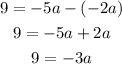
And solve for a,

`a=-3`

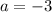
Knowing that a = -3, we can replace its value in the first equation to find b,

`b=-2a=-2(-3)=6`

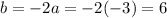
And with b = 6 we can use the second equation to find c. First, replace the values of a and b found,

`\begin{gathered} 1=4\cdot(-3)+2\cdot6+c \\ 1=-12+12+c \\ 1=c \end{gathered}`

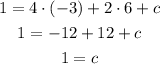
So, we got that c = 1.

Hence, the equation of the parabola described is y = -3x² + 6x + 1.