Question

A model rocket is launched straight upward with an initial speed of 25.6 m/s. It accelerates with a constant upward acceleration of 2.34 m/s2 until its engines stop at an altitude of 231 m. How long after lift-off does the rocket reach its maximum height?

Answer 1

First, let's calculate the rocket velocity when it stops accelerating, using Torricelli's equation:

`\begin{gathered} V^2=V^2_0+2\cdot a\cdot d \\ V^2=25.6^2+2\cdot2.34\cdot231 \\ V^2=655.36+1081.08 \\ V^2=1736.44 \\ V=41.67\text{ m/s}^2 \end{gathered}`

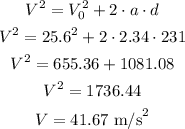
After the engine stops, the total acceleration will be the gravity acceleration, with a downwards direction and magnitude of 9.81 m/s².

The maximum height occurs when the velocity is zero, so we can use the formula below:

`\begin{gathered} V=V_0+a\cdot t \\ 0=41.67-9.81\cdot t \\ 9.81t=41.67 \\ t=(41.67)/(9.81) \\ t=4.25\text{ s} \end{gathered}`

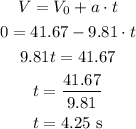
Now we need to calculate the time spent accelerating (engine turned on):

`\begin{gathered} V=V_0+a\cdot t \\ 41.67=25.6+2.34\cdot t \\ 2.34t=41.67-25.6 \\ 2.34t=16.07 \\ t=(16.07)/(2.34) \\ t=6.87\text{ s} \end{gathered}`

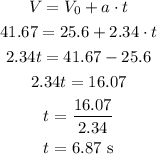
Therefore the total time, since lift-off until maximum height, is:

`\begin{gathered} t=6.87+4.25 \\ t=11.12\text{ s} \end{gathered}`

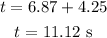
The rocket reaches the maximum height 11.12 seconds after lift-off.