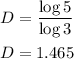Question

Compute the similarity dimension of the fractal. Round to the nearest thousandth.

Answer 1

1.465

Explanation:

The generator of the Sierpinski carpet consists of 20 line segments and the initiator consists of 4 ine segment. Thus the replacement ratio is 20:4 or 5.

The initiator of the Sierpinski carpet is a line segment that is 3 times as long as the replica line segments in the generator. Thus the scaling ratio is 3:1 or 3.

The similarity dimension D of a stricty-similar fractal is given by:

`D=(\log N)/(\log r)`

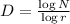
Where N is the replacement ratio of the fractal and r is the scaling ratio. Hence, the similarity dimension D of Sierpinski carpet is:

`\begin{gathered} D=(\log 5)/(\log 3) \\ D=1.465 \end{gathered}`